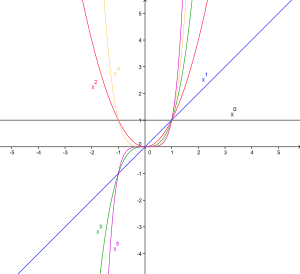
Ступенная функцыя

Ступе́нная[1], або ступе́невая[2] фу́нкцыя — функцыя выгляду , дзе (паказчык, або паказчык ступені) — некаторы рэчаісны лік[3]. Да ступенных часта прылічваюць і функцыі выгляду , дзе k — нейкі множнік расцяжэння[4]. Існуе таксама камплекснае абагульненне ступеневай функцыі. На практыцы паказчык ступені амаль заўсёды з’яўляецца цэлым ці рацыянальным лікам.
Рэчаісная ступенная функцыя
[правіць | правіць зыходнік]Абсяг вызначэння
[правіць | правіць зыходнік]- Калі паказчык ступені — цэлы лік, то ступенную функцыю можна вызначыць на ўсёй лікавай прамой (магчыма, акрамя нуля).
- Калі , дзе — узаемна простыя лікі, — няцотны, то ступенная функцыя таксама вызначана пры любых рэчаісных x (магчыма, акрамя нуля).
- У агульным выпадку ступенная функцыя вызначана толькі пры (у абсяг вызначэння можа ўваходзіць і нуль, гл. ніжэй).
- Калі , то функцыя вызначана таксама і пры .
- Пры нуль ёсць асаблівым пунктам ступеннай функцыі.
Рацыянальны паказчык ступені
[правіць | правіць зыходнік]- Графікі ступеннай функцыі пры натуральным паказчыку n называюцца парабаламі парадку n. Пры атрымліваецца лінейная функцыя , называная прамой прапарцыйнай залежнасцю.
- Графікі функцый выгляду , дзе n — натуральны лік, называюцца гіпербаламі парадку n. Пры атрымліваецца функцыя , называная адваротнай прапарцыйнай залежнасцю.
- Калі , то функцыя ёсць арыфметычным коранем ступені n.
Прыклад: з трэцяга закону Кеплера вынікае, што перыяд T абарачэння планеты вакол Сонца звязаны з вялікай паўвоссю A яе арбіты наступным чынам: (паўкубічная парабала).
-
Парабалы парадку n: -
Гіпербалы парадку n:
Уласцівасці
[правіць | правіць зыходнік]- Функцыя непарыўная і бясконца дыферэнцавальная ва ўсіх кропках, у наваколлі якіх яна вызначана. Нуль, увогуле кажучы, ёсць асаблівым пунктам.
Напрыклад, функцыя вызначана ў нулі і яго правым наваколлі, але яе вытворная у нулі не вызначана.
- На прамежку функцыя манатонна нарастае пры і манатонна спадае пры . Значэнні функцыі на гэтым прамежку дадатныя.
- Вытворная:
.
- Першаісная:
- Калі , то
- Калі , маем
Камплексная ступенная функцыя
[правіць | правіць зыходнік]У агульным выпадку ступенная функцыя камплекснай зменнай z азначаецца як[5]:
Тут паказчык ступені c — некаторы камплексны лік. Значэнне функцыі, адпаведнае галоўнаму значэнню лагарыфму, называецца галоўным значэннем ступені. Напрыклад, значэнне роўнае , дзе k — адвольны цэлы, а яго галоўнае значэнне роўнае .
Камплексная ступенная функцыя істотна адрозніваецца ад свайго рэчаіснага адменніку. З-за мнагазначнасці камплекснага лагарыфму яна, увогуле кажучы, таксама мае бясконца многа значэнняў. Аднак два выпадкі, важныя ў прыкладаннях, разглядаюцца асобна:
- Пры натуральным паказчыку ступені функцыя адназначная і n-лістная[6].
- Калі паказчык ступені — дадатны рацыянальны лік, г.зн. (нескарачальны) дроб , то функцыя будзе мець q розных значэнняў[5].
Гл. таксама
[правіць | правіць зыходнік]Крыніцы
[правіць | правіць зыходнік]- ↑ БелЭн 2002.
- ↑ Матэматычная энцыклапедыя. / Гал. рэд. В. Бернік. — Мн.: Тэхналогія, 2001. — С. 330.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Том I, §48: Важнейшие классы функций..
- ↑ Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978. — С. 312.
- ↑ а б Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Том II, стр. 526-527..
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — С. 88. — 304 с.
Літаратура
[правіць | правіць зыходнік]- Ступе́нная фу́нкцыя // Беларуская энцыклапедыя: У 18 т. Т. 15: Следавікі — Трыо / Рэдкал.: Г. П. Пашкоў і інш. — Мн. : БелЭн, 2002. — Т. 15. — С. 223. — 10 000 экз. — ISBN 985-11-0035-8. — ISBN 985-11-0251-2 (т. 15).
- Алгебра: вучэб. дапам. для 11-га кл. устаноў агул. сярэд. адукацыі з беларус. мовай навучання Архівавана 27 чэрвеня 2023. / А. П. Кузняцова[і інш.]; пад рэд. праф. Л. Б. Шнэпермана; пер. з рус. мовы Н. М. Алганавай. — 2-е выд., выпр. і дап. — Мінск: Нар. асвета, 2013. — 287 с.: іл. — 16 100 экз. — ISBN 978-985-03-1983-8.
- Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5. — С. 208-209.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — изд. 6-е. — М.: Наука, 1966.
- Степенная фунуция // Большая советская энциклопедия : ([в 30 т.]) / гл. ред. А. М. Прохоров. — 3-е изд.. — М. : Советская энциклопедия, 1969—1978. (руск.)
Спасылкі
[правіць | правіць зыходнік] На Вікісховішчы ёсць медыяфайлы па тэме Ступенная функцыя
На Вікісховішчы ёсць медыяфайлы па тэме Ступенная функцыя